多腕バンディット問題：『ゼロから作るDeep Learning ❹ ー 強化学習編』の勉強ノート(1)

はじめに

『ゼロから作るDeep Learning ❹ ー 強化学習編』で強化学習を勉強しながら、気になったことや試してみたことをまとめたノートです。備忘録として、勉強した内容を自分なりにまとめています。この記事に関しては、本と一緒に読むことを前提としています。

今回は１章「バンディット問題」を扱います。

強化学習について

ここでは、強化学習の概要について軽く解説します。まず、「強化学習（Reinforcement Learning）」は「機械学習（Machine Learning）」の手法の一つです。「機械学習とは何か？」については深入りせずにその分類と強化学習の特徴を説明していきます。

機械学習の分類

機械学習で使われる手法は解くべき問題の構造によって「教師あり学習（Supervised Learning）」「教師なし学習（Unsupervised Learning）」「強化学習（Reinforcement Learning）」の３つに分けることができます。ここでは「教師あり/なし学習」についての詳しい説明はせず、特徴だけを載せておきます。

• 教師あり学習: 正解を用意した学習データを用いて、入力から出力への変換方法を学習する。
• 教師なし学習: 正解が用意されていない入力データからそのパターンや特徴を抽出する。

機械学習といえば「教師あり/なし学習」を指すこともありますが、実は強化学習にはこれらの手法とは大きく異なる点があります。

強化学習の特徴

結論から言うと、強化学習では、エージェントが環境との相互作用の中で試行錯誤しながら学習します。以下では、これについて解説していきます。

エージェントと環境の相互作用

強化学習では、「エージェント（Agent）」が「環境（Environment）」と相互にやりとりを行います。ここで、エージェントとは意思決定及び行動の主体のことを指します。エージェントはある環境のもとに置かれており、その環境の「状態（State）」を観測し、それに基づき「行動（Action）」を行います。エージェントの行動によって環境が変化し、それに対してエージェントは環境から「報酬（Reward）」を受け取ります（同時に新たな状態も観測します）。この繰り返しが、強化学習におけるエージェントと環境の相互作用です。

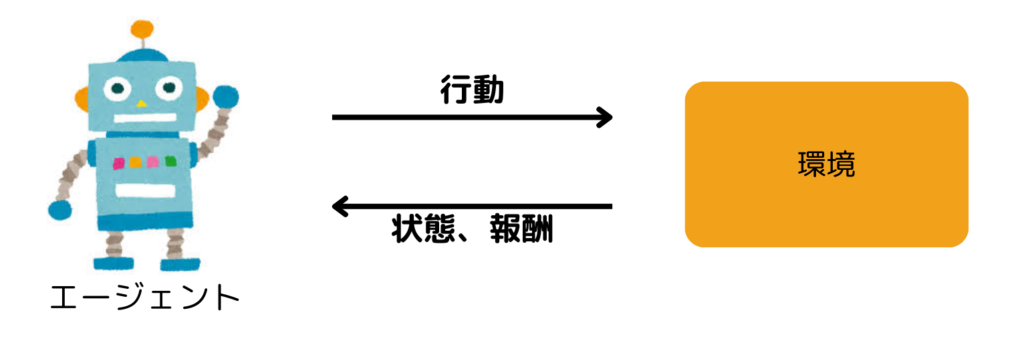
これは、エージェントをお掃除ロボットとして考えるとわかりやすいと思います。「センサーで周囲（環境）の状態を観測し、ゴミのある場所に移動する（行動）。その結果、部屋（環境）が綺麗になり、ロボット（エージェント）は報酬を受け取る。これを繰り返す。」みたいな感じ。とにかく、エージェントが主体的に行動して環境に変化を及ぼし、それに対するフィードバックとして報酬を受け取っているということが重要です。

強化学習における「学習」

強化学習では、「何が」「何を」学習しているのでしょうか？

先程はさらっと流しましたが、エージェントは観測した状態に基づいて行動を行います。この行動判断はどのように行われるのでしょうか？

実は、この行動判断を最適化することが強化学習における学習です。ここでの最適化というのは、より報酬がもらえる行動を選択するということです。つまり、強化学習の目標は、エージェントが得る報酬の総和を最大にする行動パターンを身につけることです。

再び、お掃除ロボットの例を考えてみましょう。お掃除ロボットはゴミを取ると報酬が得られることを学習しているので、ゴミを見つけると一直線に向かっていきます。しかし、その直線上に障害物があるとどうでしょう？ここで、「障害物にぶつかったら得られる報酬が減る（もしくはマイナスの報酬が与えられる）」という条件を与えてみます。まず、エージェントはぶつかりながらゴミを取りに行き、いつもより少ない報酬を得ます。すると、次回からは報酬を最大化するために障害物を避けてゴミを取りに行くようになります。お掃除ロボットが試行錯誤してデータを集め、それを元により良い行動を学習したといえますね。

強化学習の「学習」においては、エージェントが行動を行い、報酬を得ることでデータを集めます。そして、このデータを用いてより良い(報酬の多くなる)行動パターンを学習します。これを繰り返しながら（試行錯誤をしながら）、行動パターンを改善していくのが強化学習なのです。環境との相互作用の中で、試行錯誤しながら学習をしていくのは、人間の学習や発達の過程と似たものがありますね。

「教師あり/なし学習」との違い

最後に、「強化学習」と「教師あり/なし学習」の大きな違いについて説明します。「機械学習」に欠かせないものといえばなんでしょう？ それは「データ」です。データがなければ何も学習することはできませんね。

「教師あり/なし学習」においては人間がデータを用意します。少なくとも、入力データはあるので、そこから学習を開始することができます。

しかし、強化学習では人間から与えられる入力データはありません。そこで、エージェントは試行錯誤することによりデータを集めるのです。これが、強化学習の他の手法とは大きく異なる点です。

まとめると、環境との相互作用の中で学ぶこと、試行錯誤から学ぶこと、これこそが強化学習なのです。

多腕バンディット問題

ここからが本題です。強化学習の具体的な問題として、多腕バンディット問題を見ていきます。これは強化学習で扱う問題の中でも最もシンプルな問題の１つです。（教師あり）機械学習における線形回帰みたいなものですね。

多腕バンディット問題とは

まず、多腕バンディット問題（Multi-armed Bandit Problem）の概要について説明します。「バンディット（Bandit）」とはスロットマシンのことです。多腕とはスロットマシンの腕(レバー)が複数あることですが、ここではレバーが一本のスロットが複数台ある状況を考えます。また、以下ではこの問題を単にバンディット問題（Bandit Problem）と呼びます。

バンディット問題では、複数台あるマシンのそれぞれで、当たりの確率が異なります。この状態で、プレイヤーは決められた回数スロットをプレイします。プレイヤーは最初、どのスロットが当たりの確率が高いのかわからないので、プレイする中でそれを探っていきます。決められた回数の中で、どのようにして得られるコインの枚数を多くするのかがこの問題の主題です。

バンディット問題における強化学習

バンディット問題において、エージェントはプレイヤー、環境はスロットマシンです。エージェントが行動（スロットマシンを選択）することにより、報酬（コイン）を受け取ります。では、状態はどうなっているのでしょうか？

実は、バンディット問題では、環境の状態が変化しません。つまり、エージェントと環境がやりとりするのは行動（選択）と報酬（コイン）だけなのです。強化学習において最も単純な問題設定であることがわかりますね。

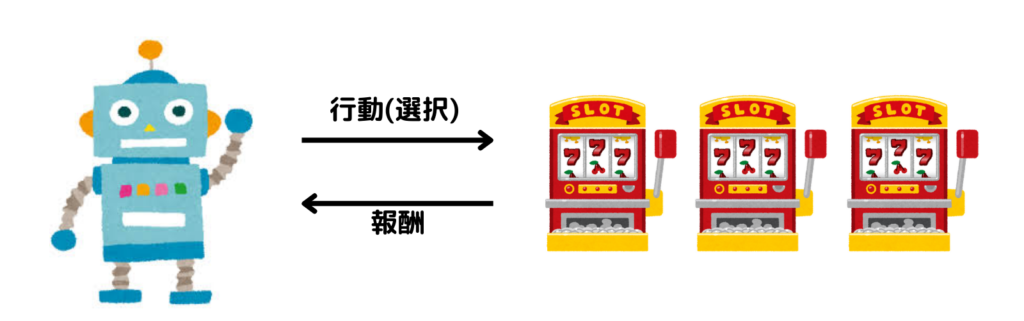
これで、バンディット問題を強化学習の枠組みに当てはめることができました。あとはエージェントが報酬を最大化する行動パターンを身につければ、バンディット問題を「解く」ことができますね。

良いスロットマシンとは

バンディット問題を解くアルゴリズムを考えるにあたって、プレイヤーが選ぶべき「良いスロットマシン」とは何かについて知る必要があります。スロットマシンの「良さ」とはなんでしょうか？

期待値

スロットマシンにはランダム性があります。一回プレイして当たり（ハズレ）が出たらそれは良い（悪い）スロットマシンなのでしょうか？ そうではありませんね。では、複数回プレイしてもらえるコインの枚数の平均を取るとどうでしょう。回数を増やすにつれて、その値はスロットマシンごとに一定の値に近づいていきます。この値こそ「期待値（Exception Value）」です。

バンディット問題では、報酬の期待値のことを価値（Value）と呼ぶ場合があります。特に「行動に対して得られる報酬の期待値」は行動価値（Action Value）と呼ばれます。以下では、単に価値と呼ぶこととします。

スロットマシンの価値(理論)

スロットマシンの価値を数式を使って表してみましょう。

本と同じ設定を考えます。報酬（Reward）を $R$ とすると、取りうる値が $\{0, 1, 5, 10\}$ の確率変数になります。　エージェントがスロットマシンa, bを選択することをそれぞれa, bとします。エージェントの行動（Action）を $A$ とすると、取りうる値が $\{a, b\}$の確率変数になります。ここでは、確率変数の定義について深入りしないでおきます。

このとき、報酬$R$の期待値（Exception Value）は $\mathbb{E}[R]$ と書けます。また、$A$ という行動を選んだ場合の報酬の期待値は $\mathbb{E}[R|A]$ と書けます。これこそが、スロットマシンの(行動)価値です。ここでは、

$$ q(A) = \mathbb{E}[R|A] \notag$$

として行動$A$の価値を表します。また、推定値の場合は$Q(A)$で表します。一般に、真の値を小文字、推定値を大文字で表すようです。

$A$に対し、$R$ の確率分布が与えられている場合、(真の)価値 $q(A)$ は次のように求められます。

$$ q(A) = \mathbb{E}[R|A] = \sum_{r \in \{0, 1, 5, 10\}} r P_A(R=r) \label{eq:e}$$

ここで、$P_A(R) = P(R|A)$です。条件付き確率関数 $p_{R|A}$の方がよかったかも。意味がわかればよしとしておいてください。

スロットマシンの価値(実装)

とりあえずスロットマシンa, bの報酬$R$の確率分布を本と同じように設定します

import numpy as np
import matplotlib.pyplot as plt

# 報酬
R = np.array([0, 1, 5, 10])

# 確率分布
P_a = np.array([0.7, 0.15, 0.12, 0.03])
P_b = np.array([0.5, 0.4, 0.09, 0.01])

確率分布をグラフにしてみます。

left = np.arange(len(R)) # 横軸
fig, ax = plt.subplots(1, 2, figsize=(8,4))

# aの棒グラフ
ax[0].bar(left, P_a, tick_label=R)
ax[0].set_ylim(0,1)
ax[0].set_xlabel('Reward')
ax[0].set_title('a')

# bの棒グラフ
ax[1].bar(left, P_b, tick_label=R)
ax[1].set_ylim(0,1)
ax[1].set_xlabel('Reward')
ax[1].set_title('b')

plt.show()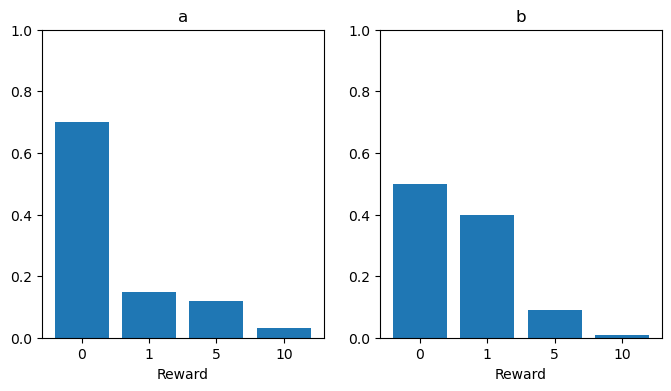

一見、bの方が良さそうに見えますが、5や10の確率を見るとaの方が良さそうです（横軸を均等にした方がわかりやすかったかも）。では、期待値を確認してみましょう。式(\ref{eq:e})の計算をするにはRとP_a, P_bの内積を求めればいいですね。

E_a = np.dot(R, P_a)
E_b = np.dot(R, P_b)
print(f'{E_a = }, {E_b = }')

E_a = 1.05, E_b = 0.95

スロットマシンaの方が価値が高いことがわかりました。

価値の推定

スロットマシンごとに報酬の確率分布が分かっている場合はその価値(期待値)を計算することができました。しかし、バンディット問題において、プレイヤーがそれを知ることはできません。そこで、実際にプレイした結果から、スロットマシンの価値を推定する必要があります。

価値の推定方法

期待値の説明のときに、複数回の結果の平均を取るという話をしました。これこそが、価値の推定方法です。

実際に得られた報酬の平均値は標本平均なので、サンプリング回数が増えるに従い真の値（報酬の期待値）に近づき、無限回の極限で真の値に一致します（大数の法則）。

１台のスロットマシンを $n$ 回プレイした場合を考えると、その時点での行動価値の推定値は

$$ Q_n = \frac{R_1+R_2+\cdots +R_n}{n} \notag $$

となります。ここで、$R_i $ は実際に得られた報酬です。これをそのまま実装したいところですが、改善点がありますね。このままだと、$n$ が大きくなるにつれて $R$ の要素数が大きくなり、計算量とメモリの使用量が増えてしまいます。そこで、$Q_{n-1}$を使って $Q_n$ を表してみましょう。

$$ Q_{n-1} = \frac{R_1+R_2+\cdots +R_{n-1}}{n-1} \notag$$

なので

\begin{align*}
Q_n &= \frac{R_1+R_2+\cdots +R_{n-1}+R_n}{n} \\
&= \frac{1}{n}\{(n-1)Q_{n-1} +R_n\} \\
&= (1-\frac{1}{n})Q_{n-1} + \frac{1}{n}R_n
\end{align*}

となります。$Q_n$ の漸化式ができました。これで、過去の $R$ を全て保持する必要がなくなります。あとは、更新する量がわかりやすいように

$$ Q_n = Q_{n-1} + \frac{1}{n}(R_n \,-\, Q_{n-1})\label{eq:Q}$$

としておきます。

価値の推定(実装)

まずは、スロットマシンを複数回プレイしてみます。np.random.choice()を使います。

# プレイ回数
N = 2000

R_a = np.random.choice(R, size=N, p=P_a)
R_b = np.random.choice(R, size=N, p=P_b)

報酬の分布を見てみましょう。

plt.figure(figsize=(5, 4))
plt.bar(left, R_a_count, tick_label=R)
plt.title('a')
plt.xlabel('Reward')
plt.ylabel('count')
plt.ylim(0, 2000)
plt.show()

plt.figure(figsize=(5, 4))
plt.bar(left, R_b_count, tick_label=R)
plt.title('b')
plt.xlabel('Reward')
plt.ylim(0, 2000)
plt.show()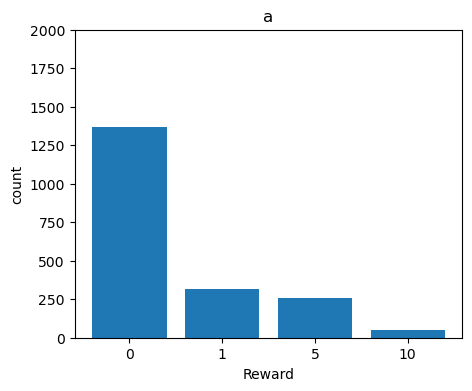

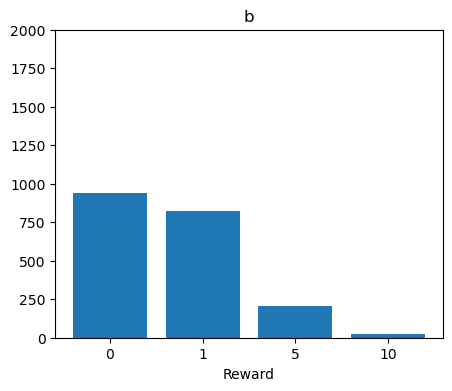
先ほどの確率分布と同じような形になっていることがわかりますね。回数が増えるにつれ、報酬の各値の出現割合が真の値（確率）に近づいていく様子をアニメーションで見てみます。

from matplotlib.animation import FuncAnimation

fig = plt.figure(figsize=(4, 4))

def update(i):
    if i != 0:
        plt.cla()
    n = 4 * i + 1
    R_rate = [np.count_nonzero(R_A[:n] == r) / n for r in R]
    plt.bar(left, R_rate, tick_label=R)
    plt.scatter(left, P_A)
    plt.title(f'{n=}')
    plt.ylim(0, 1)

R_A = R_a
P_A = P_a

anim = FuncAnimation(fig, update, frames=(N//16), interval = 120)
anim.save("anim_a.gif")

R_A = R_b
P_A = P_b

anim = FuncAnimation(fig, update, frames=(N//16), interval = 120)
anim.save("anim_b.gif")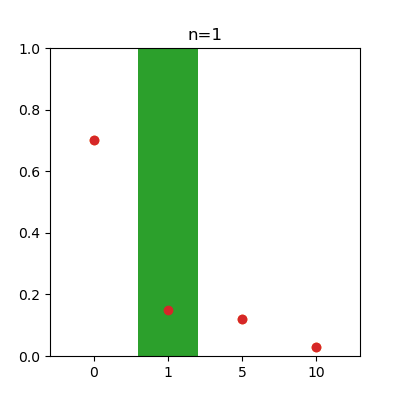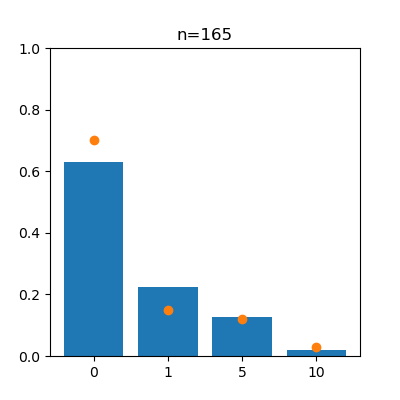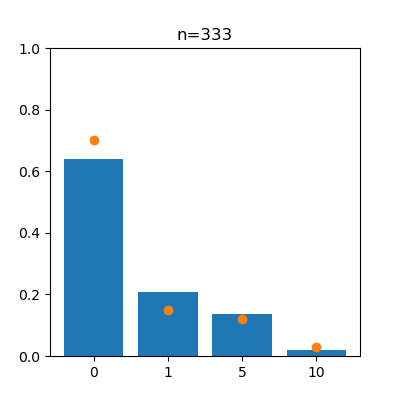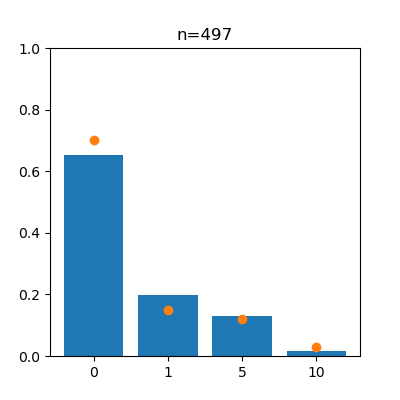

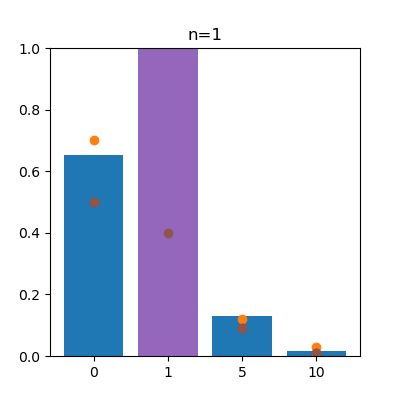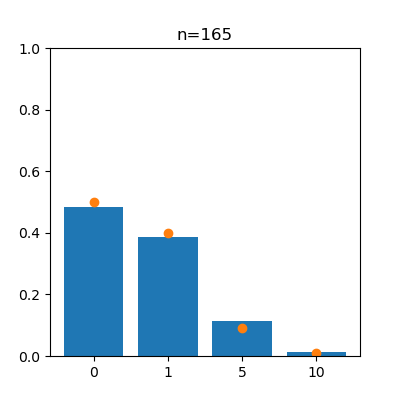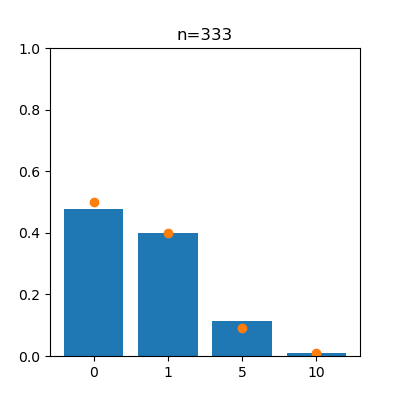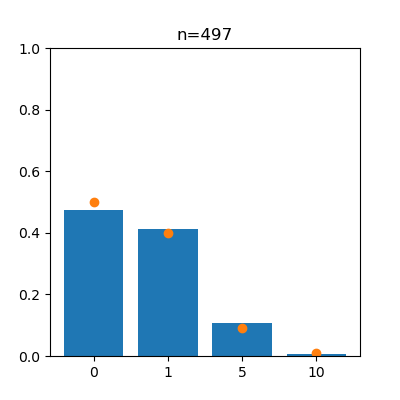
左がスロットa、右がスロットbで、オレンジの点は真の値を表しています。

さて、本題です。スロットマシンの価値の推定値を求めていきましょう。式(\ref{eq:Q})を実装します。

# プレイ回数
N = 1000
Q = 0
Q_trace = []

for n in range(1, N+1):
    reward = np.random.choice(R, p=P_a)
    Q += (reward - Q) / n
    Q_trace.append(Q)

式(\ref{eq:Q})を用いたインクリメンタル（逐次的）な実装ができました。これで、価値の推定値 $Q(a)$ を効率的に求めることができます。さて、求めた推定値が真の価値 $q(a)$ にどれだけ近づくのかを見てみましょう。

plt.plot(range(1, N+1), Q_trace, label='Q(a)')
plt.hlines(y=E_a, xmin=0, xmax=N, color='red', linestyles='dashed', label='q(a)')
plt.legend()
plt.show()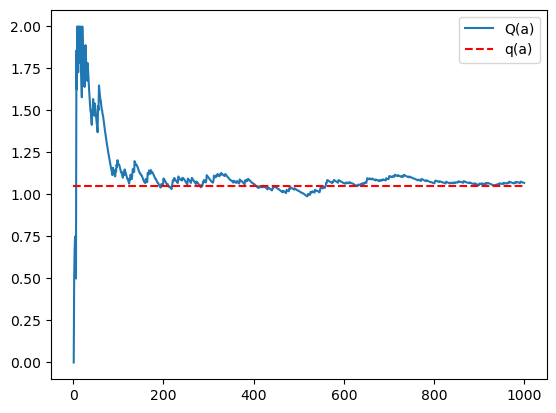

100回ぐらいから真の価値に近づいていっていることがわかりますね。以上でスロットマシンの価値を推定する方法がわかりました。

プレイ回数を増やせば増やすほど推定の精度は上がります。しかし、推定にプレイ回数を使い過ぎると報酬を増やすことができません。バランスが重要になりそうですね。次回はこの部分に注目して、バンディットアルゴリズムについて見ていきます。

おまけ

スロットマシンを実装して、実際に遊んでみます。どちらがスロットマシンaか分かっていると面白くないのでシャッフルしました。x, yはa, bのいずれかです。

import numpy as np
import random
import tkinter as tk

R = np.array([0, 1, 5, 10])
P_a = np.array([0.7, 0.15, 0.12, 0.03])
P_b = np.array([0.5, 0.4, 0.09, 0.01])
P_xy = random.sample([P_a, P_b], 2)


count = 0
total_reward = 0

def play(bandit):
    global count, total_reward
    count += 1
    reward = np.random.choice(R, p=P_xy[bandit])
    label_n['text'] = f'n: {count}'
    label_cr['text'] = f'current_reward: {reward}'
    total_reward += reward
    label_tr['text'] = f'total_reward: {total_reward}'
    label_ar['text'] = f'avg_reward: {total_reward/count:.2f}'

root = tk.Tk()
root.title('bandit')
root.geometry('120x180')

btn_x = tk.Button(root, text='x', command=lambda: play(0))
btn_x.pack()
btn_y = tk.Button(root, text='y', command=lambda: play(1))
btn_y.pack()

label_n = tk.Label(root, text=f'n: {count}')
label_n.pack()
label_cr = tk.Label(root, text='current_reward:  ')
label_cr.pack()
label_tr = tk.Label(root, text='total_reward: 0')
label_tr.pack()
label_ar = tk.Label(root, text='avg_reward:  ')
label_ar.pack()

root.mainloop()

avg_rewardが1を超えているので良さそうです。期待値を計算しながらプレイするつもりでしたが、一度10が出たxの方に突っ込んでしまいました。いい時は、回数が100を超えてもavg_rewardが1.4くらいありました（期待値が収束してないのはあまり良くない気がするけど）。ぜひ挑戦してみてください。

まとめ

まず、強化学習の特徴を復習します。

他の機械学習手法とは違って、データが与えられていないので、エージェントが自らデータを集めるのが大きな特徴ですね。

次に、バンディット問題についてです。

「良いスロットマシンとは何か」や行動価値の推定値を効率的に求める実装について学習しました。

次回からは、バンディット問題の本題ともいえる、バンディットアルゴリズムについてみていきます。

感想

これが初投稿の記事になります ^_^

自分なりにまとめるのって難しいですね。詳しく書こうとすると、だんだん本の内容の丸写しみたいになってしまう。もっと行間のある本を使った方が良かったかも。今回は文章による説明が多かったので疲れました。もっと数式やコードを書きたい！

参考文献

[1] 斎藤康毅『ゼロから作るDeep Learning ❹ ー 強化学習編』オライリー・ジャパン, 2022.

概念、数式、コードの解説がこれ以上ないほど丁寧にわかりやすく書かれています。1巻から3巻を読んでいなくても全く問題はないようになっています。